PyTorch image classifier
Posted on Thu 26 April 2018 in Projects
In [1]:
from __future__ import print_function
import torch
Tensor oprations ref: http://pytorch.org/docs/stable/torch.html¶
In [2]:
# track computations with required_grad=True:
x = torch.ones(2, 2, requires_grad=True)
print(x)
In [3]:
y = x + 2
print(y)
In [4]:
# y was created as a result of an operation, so it has a grad_fn:
print(y.grad_fn)
In [5]:
# more operations on y:
z = y * y * 3
out = z.mean()
print(z, out)
In [6]:
# backprop:
out.backward()
In [7]:
print(x.grad)
Let's call the out Tensor "o". We have that¶
\begin{equation*}
o = \frac{1}{4}\sum_{i} z_i \;\; and \;\; z_i = 3(x_i + 2)^2 \;\; and \;\;\left.z_i\right|_{x_i = 1}=27.
\end{equation*}Therefore \begin{equation*} \frac{\partial o}{\partial x_i}=\frac{3}{2}(x_i+2), \;\; hence \;\; \left.\frac{\partial o}{\partial x_i}\right|_{x_i=1}=\frac{9}{2}=4.5 \end{equation*}
In [8]:
x = torch.rand(5,3)
print(x)
In [9]:
x = x.new_ones(5, 3, dtype=torch.double)
print(x)
In [10]:
print(x.size())
In [15]:
# (in place operations are post-fixed with _)
In [16]:
# standard numpy-like indexing works:
In [17]:
print(x[:,1])
Neural Nets in PyTorch¶
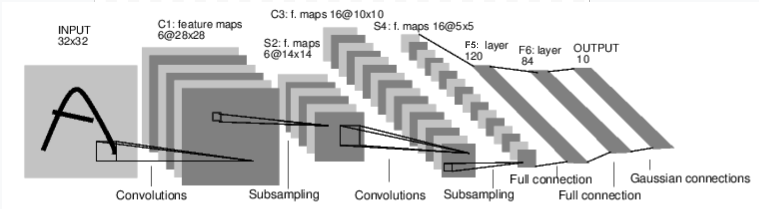
A typical training procedure for a neural network is as follows:
- Define the neural network that has some learnable parameters (or weights)
- Iterate over a dataset of inputs
- Process input through the network
- Compute the loss (how far is the output from being correct)
- Propagate gradients back into the network’s parameters
- Update the weights of the network, typically using a simple update rule:
weight = weight - learning_rate * gradient
Traning an image classifier:¶
1. Load and normalize CIFAR10 training and test datasets using torchvision (instead of boilerplate Pillow or OpenCV code)¶
In [18]:
import torchvision
import torchvision.transforms as transforms
In [19]:
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./pytorchdata', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='./pytorchdata', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
shuffle=False, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
show some of the training images, for fun:¶
In [21]:
import matplotlib.pyplot as plt
import numpy as np
def imshow(img):
img = img / 2 + 0.5 # unnormalize
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()
# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))
2. Define a Convolution Neural Net¶
It should take 3-channel images:
In [22]:
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
3. Define a Loss function and optimizer¶
Use Classification Cross-Entropy loss and SGD with momentum:
In [23]:
import torch.optim as optim
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
4. Train¶
In [24]:
for epoch in range(2): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the inputs
inputs, labels = data
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
5. Test¶
predict the class label that the neural network outputs, and check it against the ground-truth. If the prediction is correct, we add the sample to the list of correct predictions.
First, display an image from the test set to get familiar.
In [25]:
dataiter = iter(testloader)
images, labels = dataiter.next()
# print images
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))
In [26]:
# what does neural network think these examples are?
outputs = net(images)
In [27]:
print(outputs)
In [29]:
_, predicted = torch.max(outputs, 1)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]
for j in range(4)))
In [30]:
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 10000 test images: %d %%' % (
100 * correct / total))
That looks waaay better than chance, which is 10% accuracy (randomly picking a class out of 10 classes). Seems like the network learnt something.
Hmmm, what are the classes that performed well, and the classes that did not perform well:
In [31]:
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs, 1)
c = (predicted == labels).squeeze()
for i in range(4):
label = labels[i]
class_correct[label] += c[i].item()
class_total[label] += 1
for i in range(10):
print('Accuracy of %5s : %2d %%' % (
classes[i], 100 * class_correct[i] / class_total[i]))