DCP Notebook
Posted on Sun 20 May 2018 in Projects
DS [Probability, Unfair Coin]¶
There is a fair coin (one side heads, one side tails) and an unfair coin (both sides tails). You pick one at random, flip it 5 times, and observe that it comes up as tails all five times. What is the chance that you are flipping the unfair coin?
U = Unfair coin
F = Fair coin
5H = 5 tails in a row
What is $P(U \mid 5H)$?
Bayes
Given a hypothesis $H$ and evidence $E$, Bayes' theorem states that the relationship between the probability of the hypothesis before getting the evidence $P(H)$ and the probability of the hypothesis after getting the evidence $P(H \mid E)$ is:
$$
\begin{array}{c}
P(H \mid E) = P(E \mid H) \frac{P(E)}{P(H)}
\end{array}
$$
Given that:
$P(H) = P(U)( = P(F)) = 0.5$
$P(E) = P(5H) = P(5H \mid U)P(U) + P(5H \mid F)P(F) = 1*0.5 + 0.5^5*0.5$
then we have: $$ \begin{array}{c} P(U \mid 5H) = \frac{P(5H \mid U)}{P(5H)}P(U) = \frac{P(5H \mid U)}{P(5H \mid U)P(U) + P(5H \mid F)P(F)}P(U) = \frac{1}{1*0.5 + 0.5^5*0.5}0.5 = 0.97 \end{array} $$
DS [Measuring user retention]¶
Assume you have the below tables on user actions. Write a query to get the active user retention by month.
user_actions
| column name | type |
|---|---|
| user_id | integer |
| event_id | string ("sign-in", "like", "comment") |
| timestamp | datetime |
In the actions table, we can first define a temporary table called "mau" to get the monthly active users by month. Then we can do a self join by comparing every user_id across last month vs. this month, using the add_months() function to compare this month versus last month, as follows:
WITH mau AS
(SELECT DISTINCT DATE_TRUNC(‘month’, timestamp) AS month, user_id FROM user_actions)
SELECT
mau.month,
COUNT(DISTINCT user_id) AS retained_users
FROM
mau curr_month
JOIN
mau last_month
ON curr_month.month = add_months(last_month.month, 1)
AND curr_month.user_id = last_month.user_id
GROUP BY 1 ORDER BY 1 ASC
DS [Min of two uniform random variables]¶
Say we have X ~ Uniform(0, 1) and Y ~ Uniform(0, 1). What is the expected value of the minimum of X and Y?
DS [Sum of consecutive numbers]¶
Given a number n, return the number of lists of consecutive positive integers that sum up to n.
For example, for n = 9, you should return 3 since the lists are: [2, 3, 4], [4, 5], and [9]. Can you do it in linear time?
def return_num_lists_conseq_pos_int(n):
count = 0 # always count the trivial case, [n]
for i in range(1, n+1):
total = 0
while total < n:
total = total + i
i += 1
if total == n:
count += 1
return count
return_num_lists_conseq_pos_int(9)
DS [Fraud detection trade-offs]¶
Assume we have a classifier that produces a score between 0 and 1 for the probability of a particular loan application being fraudulent. In this scenario:
a) what are false positives,
b) what are false negatives, and
c) what are the trade-offs between them in terms of dollars and how should the model be weighted accordingly?
a) False positives: loan applications classified with high probability of being fradulent which are actually not fraudulent.
If loan amount was for X, and the interest rate was 10%, then we've lost 10% of X.
b) False negatives: loan applications classified with low probability of being fradulent which are actually fraudulent.
If loan amount was for X, we've lost X.
c) Trade-offs: We should penalize false negatives much more severely than false positives. In this case, if weighted by revenue, 10 false positives == 1 false nagative. So, cost should weighted 10:1 for false nagatives:false positives.
DS [Ranking lists of shows]¶
How would you design a metric to compare rankings of lists of shows for a given user?
A) shows that a user is likely to play <-- popularity. Optimize here and miss enjoyable shows that aren't popular.
B) shows that a user is likely to enjoy <-- user's predicted rating. Optimize here and get shows that are niche/unfamiliar.
Metric = A + B
Tune weights with A/B testing or ML (given enough data with positive and negative labels on the end outcome).
DCP #1¶
Given a list of numbers and a number k, return whether any two numbers from the list add up to k. For example, given [10, 15, 3, 7] and k of 17, return true since 10 + 7 is 17. Bonus: Can you do this in one pass?
def check_list(list, k):
# use nested list comprehension
# add nth element to every other element, for all n
sums = [list[n] + x for x in list for n in range(len(list))]
# print(sums)
if k in sums:
return True
else:
return False
check_list([10, 15, 3, 7], 17)
check_list([10, 15, 3, 7], 19)
- Nested list comprehension
DCP #2¶
First, I wanna know how much money I could have made yesterday if I'd been trading Apple stocks all day.
So I grabbed Apple's stock prices from yesterday and put them in a list called stock_prices, where:
The indices are the time (in minutes) past trade opening time, which was 9:30am local time. The values are the price (in US dollars) of one share of Apple stock at that time. So if the stock cost $500 at 10:30am, that means stock_prices[60] = 500.
Write an efficient function that takes stock_prices and returns the best profit I could have made from one purchase and one sale of one share of Apple stock yesterday.
For example:
stock_prices = [10, 7, 5, 8, 11, 9]
get_max_profit(stock_prices)
Returns 6 (buying for 5 and selling for 11)
No "shorting"—you need to buy before you can sell. Also, you can't buy and sell in the same time step—at least 1 minute has to pass.
stock_prices = [10, 7, 5, 8, 11, 9]
def get_max_profit(stock_prices):
if len(stock_prices) < 2:
raise ValueError ('need at least 2 prices!')
# greedy, O^n
min_price = stock_prices[0]
max_profit = stock_prices[1] - stock_prices[0]
for current_time in range(1,len(stock_prices)):
current_profit = stock_prices[current_time] - min_price
max_profit = max(max_profit, current_profit)
min_price = min(min_price, stock_prices[current_time])
return(max_profit)
get_max_profit(stock_prices)
- Greedy: Suppose we could come up with the answer in one pass through the input, by simply updating the 'best answer so far' as we went. What additional values would we need to keep updated as we looked at each item in our input, in order to be able to update the 'best answer so far' in constant time?
- Edge cases treated with
raise ValueError ('error message')
DCP #3¶
Given an array of integers, return a new array such that each element at index i of the new array is the product of all the numbers in the original array except the one at i.
For example, if our input was [1, 2, 3, 4, 5], the expected output would be [120, 60, 40, 30, 24]. If our input was [3, 2, 1], the expected output would be [2, 3, 6].
Follow-up: what if you can't use division?
import numpy as np
from functools import reduce
# with division and .prod()
def product_list_v1(list):
array = np.array(list)
product_list_v1 = [int(array.prod()/x) for x in array]
return product_list_v1
print(product_list_v1([1, 2, 3, 4, 5]))
print(product_list_v1([3, 2, 1]))
# with division and reduce
def product_list_v2(list):
array = np.array(list)
product_list_v2 = [int(reduce(lambda x, y: x*y, array)/x) for x in array]
return product_list_v2
print(product_list_v2([1, 2, 3, 4, 5]))
print(product_list_v2([3, 2, 1]))
# without division
def product_list_v3(list):
array = np.array(list)
product_list_v3 = [reduce(lambda x, y: x*y, array[array != x]) for x in array]
return product_list_v3
print(product_list_v3([1, 2, 3, 4, 5]))
print(product_list_v3([3, 2, 1]))
Reduceto iteratively perform function on a list, reducing it's dimensionmapto transform a list to another list using a functionlambdafor throw-away functions- logic mapping an array
DCP #4¶
You created a game that is more popular than Angry Birds.
Each round, players receive a score between 0 and 100, which you use to rank them from highest to lowest. So far you're using an algorithm that sorts in O(n log n ) time, but players are complaining that their rankings aren't updated fast enough. You need a faster sorting algorithm.
Write a function that takes:
- a list of
unsorted_scores - the
highest_possible_scorein the game
and returns a sorted list of scores in less than O(n log n) time
Note: np.sort() is O(n log n)!
For example:
unsorted_scores = [37, 89, 41, 65, 91, 53]
HIGHEST_POSSIBLE_SCORE = 100
sort_scores(unsorted_scores, HIGHEST_POSSIBLE_SCORE)
#Returns [91, 89, 65, 53, 41, 37]
We’re defining n as the number of unsorted_scores because we’re expecting the number of players to keep climbing.
And, we'll treat highest_possible_score as a constant instead of factoring it into our big O time and space costs because the highest possible score isn’t going to change. Even if we do redesign the game a little, the scores will stay around the same order of magnitude.
import numpy as np
import random
unsorted_scores = [37, 89, 41, 65, 91, 53, 53, 1, 6, 8, 65, 0, 91]
HIGHEST_POSSIBLE_SCORE = 100
counts = np.zeros(HIGHEST_POSSIBLE_SCORE, dtype=int)
sorted_scores = ([])
def sort_scores(unsorted_scores, HIGHEST_POSSIBLE_SCORE):
for score in unsorted_scores:
counts[score] += 1
for score in range(len(counts)):
times = counts[score]
for time in range(times):
sorted_scores.append(score)
return sorted_scores[::-1]
sort_scores(unsorted_scores, 100)
- O(n)(?) sorting with "hash table", ie. array of counts
- Reversing a list with
[::-1]slicing notation in python - Sacrificing space for time
DCP #5¶
Given the root to a binary tree, implement serialize(root), which serializes the tree into a string, and deserialize(s), which deserializes the string back into the tree.
For example, given the following Node class
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
a = Node(1)
b = Node(2)
c = Node(3)
d = Node(4)
e = Node(5)
a.left = b
a.right = c
c.left = d
c.right = e
def serialize(root):
nodes = [root]
for node in nodes:
if not node:
break
nodes += [node.left, node.right]
s = list(map(lambda x: str(x.val) if x else None, nodes))
return s
serialize(a)
def deserialize(s):
tree = Node(int(s[0]))
for item in s[1:]:
if item:
tree.left = Node(int(item))
tree.right = Node(int(item))
else:
break
return tree
deserialize(serialize(a))
The following test should pass:
node = Node('root', Node('left', Node('left.left')), Node('right'))
assert deserialize(serialize(node)).left.left.val == 'left.left'
- Unfinished
- binary trees in general
- truthiness and type casting in arrays
DCP #6¶
Given an array of integers, find the first missing positive integer in linear time and constant space. In other words, find the lowest positive integer that does not exist in the array. The array can contain duplicates and negative numbers as well.
For example, the input [3, 4, -1, 1] should give 2. The input [1, 2, 0] should give 3.
You can modify the input array in-place.
array = [3, 4, -1, 1]
# array = np.array([1, 2, 0])
def find_first_missing_positive(array):
new_array = [array[0]]
for i in range(1,len(array)):
if array[i] > new_array[i-1]:
new_array.append(array[i])
else:
new_array.insert(i-1, array[i])
return(new_array)
find_first_missing_positive(array)
- Unfinished
DCP #7¶
cons(a, b) constructs a pair, and car(pair) and cdr(pair) returns the first and last element of that pair. For example, car(cons(3, 4)) returns 3, and cdr(cons(3, 4)) returns 4.
Given this implementation of cons:
def cons(a, b):
def pair(f):
return f(a, b)
return pair
Implement car and cdr.
def cons(a, b):
def pair(f):
return f(a, b)
return pair
def car(pair):
def return_first(a, b):
return a
return pair(return_first)
def cdr(pair):
def return_last(a, b):
return b
return pair(return_last)
car(cons(3, 4)), cdr(cons(3, 4))
- unfinished
DCP #7¶
Given the mapping a = 1, b = 2, ... z = 26, and an encoded message, count the number of ways it can be decoded.
For example, the message 111 would give 3, since it could be decoded as aaa, ka, and ak.
You can assume that the messages are decodable. For example, 001 is not allowed.
message = 111
DCP #8¶
A unival tree (which stands for "universal value") is a tree where all nodes under it have the same value.
Given the root to a binary tree, count the number of unival subtrees.
For example, the following tree has 5 unival subtrees:
0
/ \
1 0
/ \
1 0
/ \
1 1class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
a = Node(0)
b = Node(1)
c = Node(0)
d = Node(1)
e = Node(0)
f = Node(1)
g = Node(1)
a.left = b
a.right = c
c.left = d
c.right = e
d.left = f
d.right = g
# depth-first, simply due to recursion
def count_unival_subtrees(root):
# if no root is given, return 0
if not root:
return 0
# if root has no children, unival count is 1
elif not root.left and not root.right:
return 1
# if root.left == None and root.right exists
elif not root.left and root.val == root.right.val:
return 1 + count_unival_subtrees(root.right)
# if root.right == None and root.left exists
elif not root.right and root.val == root.left.val:
return 1 + count_unival_subtrees(root.left)
children_counts = count_unival_subtrees(root.left) + count_unival_subtrees(root.right)
# if node, node.left and node.right are all equal, that counts too:
current_note_count = 0
if root.val == root.left.val == root.right.val:
current_note_count = 1
return current_note_count + children_counts
print(count_unival_subtrees(a))
assert count_unival_subtrees(None) == 0
assert count_unival_subtrees(b) == 1
assert count_unival_subtrees(c) == 4
assert count_unival_subtrees(d) == 3
assert count_unival_subtrees(e) == 1
assert count_unival_subtrees(f) == 1
assert count_unival_subtrees(g) == 1
- recursion
DCP #16¶
You run an e-commerce website and want to record the last N order ids in a log. Implement a data structure to accomplish this, with the following API:
record(order_id): adds the order_id to the log
get_last(i): gets the ith last element from the log.
i is guaranteed to be smaller than or equal to N. You should be as efficient with time and space as possible.
log = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
def record(order_id):
log.append(order_id)
def get_last(i):
return log[-i]
def last_N_order_ids(N):
return [get_last(i) for i in range(1,N+1)]
assert last_N_order_ids(3) == [10, 9, 8], 'fail'
last_N_order_ids(3)
- python array slicing..?
DCP #20¶
Given two singly linked lists that intersect at some point, find the intersecting node. The lists are non-cyclical.
For example, given A = 3 -> 7 -> 8 -> 10 and B = 99 -> 1 -> 8 -> 10, return the node with value 8.
In this example, assume nodes with the same value are the exact same node objects.
Do this in O(M + N) time (where M and N are the lengths of the lists) and constant space.
class Node:
def __init__(self, val=None, next=None):
self.val = val
self.next = next
A = Node(3, Node(7, Node(8, Node(10))))
B = Node(99, Node(1, Node(8, Node(10))))
def find_intersection(A, B):
# enumerate A first, turn it into a list
list_a = [A.val]
while A.next:
list_a.append(A.next.val)
A = A.next
# go through B, searching for matches
while B.next:
if B.val in list_a:
return B.val
else:
B = B.next
## test
assert find_intersection(A, B) == 8
- linked lists
- O() analysis
To Do¶
Data exploration. You should have pandas functions like .corr(), scatter_matrix() , .hist() and .bar() on the tip of your tongue. You should always be looking for opportunities to visualize your data using PCA or t-SNE, using sklearn's PCA and TSNE functions.
Feature selection. 90% of the time, your dataset will have way more features than you need (which leads to excessive training time, and a heightened risk of overfitting). Get familiar with basic filter methods (look up scikit-learn’s VarianceThreshold and SelectKBest functions), and more sophisticated model-based feature selection methods (look up SelectFromModel).
Hyperparameter search for model optimization. You definitely should know what GridSearchCV does and how it works. Likewise for RandomSearchCV. To really stand out, try experimenting with skopt's BayesSearchCV to learn how you can apply bayesian optimization to your hyperparameter search.
Pipelines. Use sklearn's pipeline library to wrap their preprocessing, feature selection and modeling steps together. Discomfort with pipeline is a huge tell that a data scientist needs to get more familiar with their modeling toolkit.
Bayes’s theorem. It’s a foundational pillar of probability theory, and it comes up all the time in interviews. You should practice doing some basic Bayes theorem whiteboarding problems, and read the first chapter of this famous book to get a rock-solid understanding of the origin and meaning of the rule (bonus: it’s actually a fun read!).
Basic probability. You should be able to answer questions like these.
Model evaluation. In classification problems, for example, most n00bs default to using model accuracy as their metric, which is usually a terrible choice. Get comfortable with sklearn's precision_score, recall_score, f1_score , and roc_auc_score functions, and the theory behind them. For regression tasks, understanding why you would use mean_squared_error rather than mean_absolute_error (and vice-versa) is also crucial. It’s really worth taking the time to check out all the model evaluation metrics listed in sklearn's official documentation.
Classes¶
class Rocket():
# simulate a rocket, for a game
def __init__(self):
self.x = 0 #stores attributes of Rocket
self.y = 0
def move_up(self): #do something to one of the attributes
self.y += 1
#Now, make a Rocket:
#variable = name of the class
rocket = Rocket()
print(rocket)
rocket.x
rocket.y
rocket.move_up()
rocket.y
# Create a fleet of 5 rockets, and store them in a list.
my_rockets = []
for x in range(0,5):
new_rocket = Rocket()
my_rockets.append(new_rocket)
for rocket in my_rockets:
print(rocket)
# with list comprehension:
my_rockets_list = [Rocket() for x in range(0,5)]
print(my_rockets_list)
my_rockets_list[4].move_up()
for rockets in my_rockets_list:
print('altitude:', rockets.y)
- Making a new class
- Assigning the class attributes
- Defining methods for the class
- Accessing attributes and methods with dot notation
# accept parameters for init method
class Rocket():
def __init__(self, x=0, y=0):
self.x = x
self.y = y
def move_up(self):
self.y += 1
a = Rocket(5,10)
a.move_up()
a.y
# accept parameters for move_up method
class Rocket():
def __init__(self, x=0, y=0):
self.x = x
self.y = y
def move_rocket(self, x_increment=0, y_increment=0):
self.x += x_increment
self.y += y_increment
b = Rocket(0,0)
b.move_rocket(1,2)
print(b.x, b.y)
from math import sqrt
# add "distance to other rocket" method
class Rocket():
def __init__(self, x=0, y=0):
self.x = x
self.y = y
def move_rocket(self, x_increment=0, y_increment=0):
self.x += x_increment
self.y += y_increment
def get_distance(self, other_rocket):
x_diff = self.x-other_rocket.x
y_diff = self.y-other_rocket.y
distance = sqrt(x_diff**2 + y_diff**2)
return distance
Rocket(0,0).get_distance(Rocket(1,1))
Inheritance¶
New (child) class can inherit all methods and attributes from (parent) class, and can override or add to them.
class NewClass(ParentClass):
def __init__(self, arguments_new_class, arguments_parent_class):
super().__init__(arguments_parent_class) # Code for initializing an object of the new class.
class Shuttle(Rocket):
# Shuttle simulates a space shuttle, which is really
# just a reusable rocket.
def __init__(self, x=0, y=0, flights_completed=0):
super().__init__(x, y)
self.flights_completed = flights_completed
Modules¶
When you save a class into a separate file, that file is called a module. Many classes can be saved in one module.
# Save as rocket.py
from math import sqrt
class Rocket():
# Rocket simulates a rocket ship for a game,
# or a physics simulation.
def __init__(self, x=0, y=0):
# Each rocket has an (x,y) position.
self.x = x
self.y = y
def move_rocket(self, x_increment=0, y_increment=1):
# Move the rocket according to the paremeters given.
# Default behavior is to move the rocket up one unit.
self.x += x_increment
self.y += y_increment
def get_distance(self, other_rocket):
# Calculates the distance from this rocket to another rocket,
# and returns that value.
distance = sqrt((self.x-other_rocket.x)**2+(self.y-other_rocket.y)**2)
return distance
class Shuttle(Rocket):
# Shuttle simulates a space shuttle, which is really
# just a reusable rocket.
def __init__(self, x=0, y=0, flights_completed=0):
super().__init__(x, y)
self.flights_completed = flights_completed
Then, can import that module into a new script, say, rocket_simulation:
# inside rocket_simulation.py, do..
# from (module) import (Class)
from rocket import Rocket, Shuttle
rocket = Rocket(5, 16)
print("The rocket is at (%d, %d)." % (rocket.x, rocket.y))
shuttle = Shuttle(0, 0, 7)
print("The shuttle is at (%d, %d) and has flown %d times." % (shuttle.x, shuttle.y, shuttle.flights_completed))
- Accepting parameters in methods
- Inheritcance of attributes and methods by new class from parent class
- Saving multiple classes into a module, and importing it for use.
- Threads and Locks
- Cracking the Coding Interview
- Bayes Theorem, Basic Probability, ex. collision in hash table
Dijkstra's algorithm, and A*¶

- cost = g(x), ie. "miles from Denver to Santa Fe"
- Goal is to reach destination node with minimal g(x) + h(x), where h(x) is some heuristic, like "distance as the crow flies".
- If
h(x) = 0, Dijkstra --> A* (or is it vice versa?) - Keep track of "cost so far", and "visited nodes".
pop()¶
a = list(range(0,5))
a
a.pop()
a
a.pop()
a
a.pop(0)
a
a
in python, there is no "push", but .append() achieves the same thing:
a
a.append(3)
a
but, append() returns "None", so the editing of a is done "in-place" and it doesn't make sense to reassign it:
a
a = a.append(4)
a
a = list(range(0,5))
a
a.append(5)
a
a.pop()
a
a.extend([7, 8])
a
breadth first and depth first searching¶
graph = {'A': set(['B', 'C']),
'B': set(['A', 'D', 'E']),
'C': set(['A', 'F']),
'D': set(['B']),
'E': set(['B', 'F']),
'F': set(['C', 'E'])}
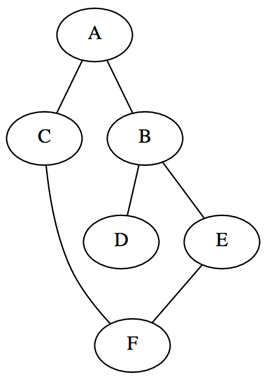
# goal: visit all nodes, depth first
def dfs(graph, start):
visited, queue = [], [start]
while queue:
vertex = queue.pop() # <--- popping off the left (.pop(0)) or right (.pop()) changes the behavior between breadth and depth, respectively.
print("current: ", vertex)
print("queue: ", queue)
if vertex not in visited:
visited.append(vertex)
print("visited: ", visited)
queue.extend(graph[vertex] - set(visited))
print("queue:", queue)
print(" ")
return visited
dfs(graph,'A')
# goal: visit all nodes, breadth first
def bfs(graph, start):
visited, queue = [], [start]
while queue:
vertex = queue.pop(0) # <--- popping off the left (.pop(0)) or right (.pop()) changes the behavior between breadth and depth, respectively.
print("current: ", vertex)
print("queue: ", queue)
if vertex not in visited:
visited.append(vertex)
print("visited: ", visited)
queue.extend(graph[vertex] - set(visited))
print("queue:", queue)
print(" ")
return visited
bfs(graph,'A')